Milliken–Taylor theorem

In mathematics, the Milliken–Taylor theorem in combinatorics is a generalization of both Ramsey's theorem and Hindman's theorem. It is named after Keith Milliken and Alan D. Taylor.

Let 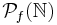$\mathcal{P}_f(\mathbb{N})$ denote the set of finite subsets of 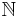$\mathbb{N}$ . Given a sequence of integers 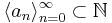$\langle a_n \rangle_{n=0}^\infty \subset \mathbb{N}$ and k > 0 let

$[FS(\langle a_n \rangle_{n=0}^\infty)]^k_< = \left \{ \left \{ \sum_{t \in \alpha_1}a_t, \ldots , \sum_{t \in \alpha_k}a_t \right \}: \alpha_1 <\cdots < \alpha_k \in \mathcal{P}_f(\mathbb{N}) \right \}$ ,

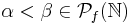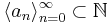where $\alpha < \beta \in \mathcal{P}_f(\mathbb{N})$ if and only if max α<min β. Let $[S]^k$ denote the k-element subsets of a set S. The Milliken–Taylor theorem says that for any finite partition $[\mathbb{N}]^k=C_1 \cup C_2 \cup \cdots \cup C_r$ , there exist some i < r + 1 and a sequence $\langle a_n \rangle_{n=0}^{\infty} \subset \mathbb{N}$ such that $[FS(\langle a_n \rangle_{n=0}^{\infty})]^k_< \subset C_i$ .

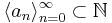For each $\langle a_n \rangle_{n=0}^\infty \subset \mathbb{N}$ , call $[FS(\langle a_n \rangle_{n=0}^\infty)]^k_<$ an MT^k set. Then, alternatively, the Milliken–Taylor theorem asserts that the collection of MT^k sets is partition regular for each k.

References

K. Milliken, Ramsey's Theorem with sums or unions, J. Comb. Theory (Series A) 18 (1975), 276–290
A. Taylor, A canonical partition relation for finite subsets of ω, J. Comb. Theory (Series A) 21 (1976), 137–146